在鑄(zhu)(zhu)錠凝固過(guo)程中(zhong),增加壓力能夠(gou)改善鑄(zhu)(zhu)型(xing)和鑄(zhu)(zhu)錠的接(jie)觸環境,為了深(shen)入研(yan)究壓力強(qiang)化鑄(zhu)(zhu)錠和鑄(zhu)(zhu)型(xing)間換熱(re)(re)的效(xiao)果,在能量(liang)(liang)守恒的基礎上(shang),運用導熱(re)(re)微分方程,建(jian)立換熱(re)(re)系(xi)(xi)數的反算(suan)模(mo)(mo)型(xing),量(liang)(liang)化壓力對(dui)換熱(re)(re)系(xi)(xi)數的影響規律(lv)。該(gai)模(mo)(mo)型(xing)包含傳(chuan)(chuan)熱(re)(re)正問題(ti)模(mo)(mo)型(xing)和傳(chuan)(chuan)熱(re)(re)反問題(ti)模(mo)(mo)型(xing)。
1.傳熱正問題(ti)模型
凝(ning)固(gu)過(guo)程(cheng)中(zhong)的(de)熱(re)(re)量(liang)(liang)傳輸是(shi)凝(ning)固(gu)進行的(de)驅動力,直接關系著(zhu)金屬(shu)液相(xiang)凝(ning)固(gu)的(de)整個(ge)進程(cheng)。凝(ning)固(gu)過(guo)程(cheng)中(zhong),熱(re)(re)量(liang)(liang)通過(guo)金屬(shu)液相(xiang)、已(yi)凝(ning)固(gu)的(de)金屬(shu)固(gu)相(xiang)、鑄錠-鑄型(xing)界(jie)面(氣隙等)和鑄型(xing)的(de)熱(re)(re)阻向環境傳輸。因存在凝(ning)固(gu)潛熱(re)(re)的(de)釋放,凝(ning)固(gu)是(shi)一個(ge)有熱(re)(re)源的(de)非穩態傳熱(re)(re)過(guo)程(cheng),基(ji)于凝(ning)固(gu)過(guo)程(cheng)熱(re)(re)傳導的(de)能(neng)量(liang)(liang)守恒原理,柱坐標(biao)下鑄錠和鑄型(xing)的(de)導熱(re)(re)分方程(cheng)可表示為:


鋼液釋放(fang)凝(ning)固潛(qian)(qian)(qian)(qian)熱(re)(re),進而在(zai)體積單(dan)元(yuan)內(nei)產(chan)生內(nei)熱(re)(re)源(yuan)q;在(zai)運用(yong)數值離散的(de)方法(fa)(fa)求解導熱(re)(re)微分方程(cheng)時,凝(ning)固潛(qian)(qian)(qian)(qian)熱(re)(re)的(de)處(chu)(chu)理(li)方法(fa)(fa)通(tong)常有四種(zhong),分別為等(deng)效(xiao)比(bi)(bi)熱(re)(re)法(fa)(fa)、熱(re)(re)焓法(fa)(fa)、溫度回升(sheng)法(fa)(fa)以及源(yuan)項(xiang)處(chu)(chu)理(li)法(fa)(fa)。孫天亮對四種(zhong)凝(ning)固潛(qian)(qian)(qian)(qian)熱(re)(re)的(de)處(chu)(chu)理(li)法(fa)(fa)進行(xing)比(bi)(bi)較發現(xian),源(yuan)項(xiang)處(chu)(chu)理(li)法(fa)(fa)最為精確,其次是(shi)等(deng)效(xiao)比(bi)(bi)熱(re)(re)法(fa)(fa),誤差較大(da)的(de)是(shi)溫度回升(sheng)法(fa)(fa)和熱(re)(re)焓法(fa)(fa);在(zai)一般(ban)情況下(xia),為了簡化計算和降低編程(cheng)難度,可采用(yong)等(deng)效(xiao)比(bi)(bi)熱(re)(re)法(fa)(fa)處(chu)(chu)理(li)凝(ning)固潛(qian)(qian)(qian)(qian)熱(re)(re)。因此,在(zai)非穩態條件下(xia),內(nei)熱(re)(re)源(yuan)與凝(ning)固潛(qian)(qian)(qian)(qian)熱(re)(re)的(de)關系可表示為:
此(ci)外,由于鑄(zhu)(zhu)(zhu)(zhu)錠的(de)凝固收縮和(he)(he)鑄(zhu)(zhu)(zhu)(zhu)型(xing)的(de)受熱(re)(re)(re)(re)(re)膨脹,鑄(zhu)(zhu)(zhu)(zhu)錠和(he)(he)鑄(zhu)(zhu)(zhu)(zhu)型(xing)接(jie)觸(chu)隨(sui)之發生變(bian)化,當鑄(zhu)(zhu)(zhu)(zhu)錠和(he)(he)鑄(zhu)(zhu)(zhu)(zhu)型(xing)間氣(qi)隙形成(cheng)以后,鑄(zhu)(zhu)(zhu)(zhu)錠向(xiang)鑄(zhu)(zhu)(zhu)(zhu)型(xing)的(de)傳(chuan)熱(re)(re)(re)(re)(re)方式不(bu)只是簡單的(de)傳(chuan)導傳(chuan)熱(re)(re)(re)(re)(re),同(tong)時(shi)存(cun)在小區域的(de)對流和(he)(he)輻射傳(chuan)熱(re)(re)(re)(re)(re),進而加(jia)大了(le)計(ji)算(suan)的(de)復(fu)雜性(xing),為(wei)了(le)降低(di)計(ji)算(suan)的(de)復(fu)雜性(xing)和(he)(he)難度,采用等效界(jie)面換(huan)熱(re)(re)(re)(re)(re)系數hi來替(ti)代(dai)氣(qi)隙形成(cheng)后鑄(zhu)(zhu)(zhu)(zhu)錠和(he)(he)鑄(zhu)(zhu)(zhu)(zhu)型(xing)間復(fu)雜的(de)傳(chuan)導、對流和(he)(he)輻射傳(chuan)熱(re)(re)(re)(re)(re)過程,在不(bu)考慮間隙比熱(re)(re)(re)(re)(re)容的(de)情況下(xia),等效界(jie)面換(huan)熱(re)(re)(re)(re)(re)系數h;計(ji)算(suan)方法如下(xia):
2. 傳(chuan)熱反問(wen)題(ti)模型(xing)
與正問題(ti)(ti)相(xiang)對應的(de)反(fan)問題(ti)(ti),即在求解傳(chuan)熱(re)問題(ti)(ti)時,以(yi)(yi)溫(wen)度場為已知(zhi)量,對邊(bian)界(jie)(jie)條(tiao)件或(huo)初(chu)始條(tiao)件進行(xing)計算的(de)過程。傳(chuan)熱(re)反(fan)問題(ti)(ti)的(de)研究(jiu)從(cong)20世紀60年代以(yi)(yi)來得到了空前的(de)進步與應用。在鑄(zhu)造過程中,鑄(zhu)錠和(he)鑄(zhu)型間邊(bian)界(jie)(jie)條(tiao)件的(de)反(fan)問題(ti)(ti)也一直備受關注。通(tong)傳(chuan)熱(re)正問題(ti)(ti)模型可知(zhi),在鑄(zhu)錠和(he)鑄(zhu)型物性(xing)參數、初(chu)始條(tiao)件以(yi)(yi)及除(chu)鑄(zhu)錠和(he)鑄(zhu)型間邊(bian)界(jie)(jie)條(tiao)件以(yi)(yi)外,其他邊(bian)界(jie)(jie)條(tiao)件可知(zhi)的(de)情況下(xia)。溫(wen)度場可表示成隨鑄(zhu)錠和(he)鑄(zhu)型間界(jie)(jie)面換熱(re)系(xi)數變化的(de)函數,即

利(li)(li)用(yong)(yong)傳(chuan)熱反問題模型,運用(yong)(yong)數值離散的(de)方法(fa)(fa)求解界(jie)面(mian)(mian)換熱系(xi)數的(de)過程,相當于(yu)依照一(yi)定的(de)方法(fa)(fa)或(huo)者規律選(xuan)定界(jie)面(mian)(mian)換熱系(xi)數,并以(yi)此作(zuo)為已知邊界(jie)條件(jian),利(li)(li)用(yong)(yong)傳(chuan)熱正問題計算出相應的(de)溫度場,如果溫度場的(de)計算值與測(ce)量(liang)值之間的(de)偏(pian)差(cha)最小,那么選(xuan)定的(de)界(jie)面(mian)(mian)換熱系(xi)數最接近(jin)真(zhen)實值。為了(le)度量(liang)溫度場計算值與測(ce)量(liang)值之間的(de)偏(pian)差(cha),利(li)(li)用(yong)(yong)最小二乘法(fa)(fa)構建以(yi)下函(han)數關(guan)系(xi)
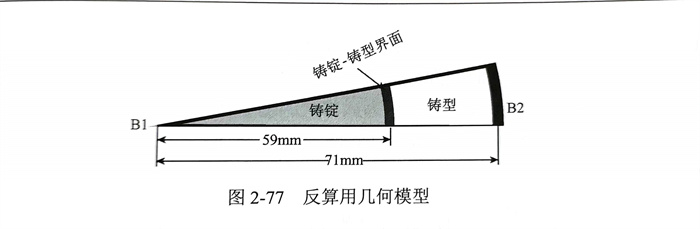
因此(ci),在給定界(jie)(jie)(jie)面(mian)(mian)換(huan)熱(re)系(xi)數(shu)初始值(zhi)的(de)(de)情(qing)況下,利(li)用式(2-151)可(ke)對界(jie)(jie)(jie)面(mian)(mian)換(huan)熱(re)系(xi)數(shu)h進行迭代(dai)(dai)求(qiu)解,每次迭代(dai)(dai)均(jun)利(li)用傳熱(re)正(zheng)問題模(mo)型(xing)對熱(re)電偶測(ce)量點的(de)(de)溫度(du)T(h)進行計(ji)算;當迭代(dai)(dai)結果滿足精(jing)度(du)要求(qiu)時,即可(ke)獲得接(jie)近界(jie)(jie)(jie)面(mian)(mian)換(huan)熱(re)系(xi)數(shu)真實值(zhi)的(de)(de)h.對于一(yi)維導熱(re)過程,界(jie)(jie)(jie)面(mian)(mian)換(huan)熱(re)系(xi)數(shu)反算模(mo)型(xing)求(qiu)解過程中(zhong)可(ke)用如(ru)圖2-77所示的(de)(de)幾何模(mo)型(xing),除了(le)鑄錠(ding)和(he)鑄型(xing)間邊(bian)界(jie)(jie)(jie)條(tiao)件以外,模(mo)型(xing)中(zhong)還包含兩個邊(bian)界(jie)(jie)(jie)條(tiao)件,分別為鑄錠(ding)心部邊(bian)界(jie)(jie)(jie)條(tiao)件(B1)和(he)外表(biao)面(mian)(mian)邊(bian)界(jie)(jie)(jie)條(tiao)件(B2).
3. 正/反傳熱問題的數(shu)值求解方法

數(shu)(shu)(shu)(shu)(shu)(shu)值離散方(fang)(fang)法(fa)(fa)主要(yao)包(bao)含有(you)(you)(you)限(xian)(xian)(xian)元、有(you)(you)(you)限(xian)(xian)(xian)體(ti)(ti)(ti)積(ji)(ji)及有(you)(you)(you)限(xian)(xian)(xian)差(cha)分(fen)(fen)(fen)法(fa)(fa)。有(you)(you)(you)限(xian)(xian)(xian)元法(fa)(fa)的(de)(de)(de)(de)基礎是變(bian)分(fen)(fen)(fen)原理和加權余量(liang)(liang)法(fa)(fa),其(qi)(qi)基本求(qiu)解(jie)(jie)思(si)想(xiang)是把(ba)(ba)計(ji)算域(yu)劃分(fen)(fen)(fen)為(wei)(wei)有(you)(you)(you)限(xian)(xian)(xian)個(ge)互不重(zhong)(zhong)疊的(de)(de)(de)(de)單(dan)元,在每(mei)個(ge)單(dan)元內,選擇一(yi)(yi)些合(he)適的(de)(de)(de)(de)節(jie)點(dian)作為(wei)(wei)求(qiu)解(jie)(jie)函數(shu)(shu)(shu)(shu)(shu)(shu)的(de)(de)(de)(de)插值點(dian),將(jiang)微(wei)分(fen)(fen)(fen)方(fang)(fang)程(cheng)(cheng)中(zhong)的(de)(de)(de)(de)變(bian)量(liang)(liang)改寫成由各變(bian)量(liang)(liang)或(huo)(huo)其(qi)(qi)導數(shu)(shu)(shu)(shu)(shu)(shu)的(de)(de)(de)(de)節(jie)點(dian)值與所(suo)選用(yong)的(de)(de)(de)(de)插值函數(shu)(shu)(shu)(shu)(shu)(shu)組成的(de)(de)(de)(de)線性表(biao)達式(shi)(shi)(shi)(shi)(shi),借(jie)助變(bian)分(fen)(fen)(fen)原理或(huo)(huo)加權余量(liang)(liang)法(fa)(fa),將(jiang)微(wei)分(fen)(fen)(fen)方(fang)(fang)程(cheng)(cheng)離散求(qiu)解(jie)(jie)。有(you)(you)(you)限(xian)(xian)(xian)體(ti)(ti)(ti)積(ji)(ji)法(fa)(fa)的(de)(de)(de)(de)基本思(si)路是將(jiang)計(ji)算區(qu)域(yu)劃分(fen)(fen)(fen)為(wei)(wei)一(yi)(yi)系列(lie)不重(zhong)(zhong)復的(de)(de)(de)(de)控制體(ti)(ti)(ti)積(ji)(ji),并使(shi)每(mei)個(ge)網格(ge)(ge)(ge)(ge)(ge)點(dian)周圍有(you)(you)(you)一(yi)(yi)個(ge)控制體(ti)(ti)(ti)積(ji)(ji);將(jiang)待解(jie)(jie)的(de)(de)(de)(de)微(wei)分(fen)(fen)(fen)方(fang)(fang)程(cheng)(cheng)對每(mei)一(yi)(yi)個(ge)控制體(ti)(ti)(ti)積(ji)(ji)積(ji)(ji)分(fen)(fen)(fen),便得出一(yi)(yi)組離散方(fang)(fang)程(cheng)(cheng)。其(qi)(qi)中(zhong)的(de)(de)(de)(de)未知(zhi)數(shu)(shu)(shu)(shu)(shu)(shu)是網格(ge)(ge)(ge)(ge)(ge)點(dian)上因(yin)變(bian)量(liang)(liang)的(de)(de)(de)(de)數(shu)(shu)(shu)(shu)(shu)(shu)值。有(you)(you)(you)限(xian)(xian)(xian)差(cha)分(fen)(fen)(fen)法(fa)(fa)是將(jiang)求(qiu)解(jie)(jie)域(yu)劃分(fen)(fen)(fen)為(wei)(wei)差(cha)分(fen)(fen)(fen)網格(ge)(ge)(ge)(ge)(ge),用(yong)有(you)(you)(you)限(xian)(xian)(xian)個(ge)網格(ge)(ge)(ge)(ge)(ge)節(jie)點(dian)代(dai)替連(lian)續的(de)(de)(de)(de)求(qiu)解(jie)(jie)域(yu),以泰勒級數(shu)(shu)(shu)(shu)(shu)(shu)展開等方(fang)(fang)法(fa)(fa),把(ba)(ba)控制方(fang)(fang)程(cheng)(cheng)中(zhong)的(de)(de)(de)(de)導數(shu)(shu)(shu)(shu)(shu)(shu)用(yong)網格(ge)(ge)(ge)(ge)(ge)節(jie)點(dian)上函數(shu)(shu)(shu)(shu)(shu)(shu)值的(de)(de)(de)(de)差(cha)商(shang)代(dai)替進行(xing)離散,從而(er)建立(li)以網格(ge)(ge)(ge)(ge)(ge)節(jie)點(dian)上的(de)(de)(de)(de)值為(wei)(wei)未知(zhi)數(shu)(shu)(shu)(shu)(shu)(shu)的(de)(de)(de)(de)代(dai)數(shu)(shu)(shu)(shu)(shu)(shu)方(fang)(fang)程(cheng)(cheng)組。對于有(you)(you)(you)限(xian)(xian)(xian)差(cha)分(fen)(fen)(fen)格(ge)(ge)(ge)(ge)(ge)式(shi)(shi)(shi)(shi)(shi),從格(ge)(ge)(ge)(ge)(ge)式(shi)(shi)(shi)(shi)(shi)的(de)(de)(de)(de)精度來劃分(fen)(fen)(fen),有(you)(you)(you)一(yi)(yi)階格(ge)(ge)(ge)(ge)(ge)式(shi)(shi)(shi)(shi)(shi)、二階格(ge)(ge)(ge)(ge)(ge)式(shi)(shi)(shi)(shi)(shi)和高階格(ge)(ge)(ge)(ge)(ge)式(shi)(shi)(shi)(shi)(shi)。從差(cha)分(fen)(fen)(fen)的(de)(de)(de)(de)空間(jian)形式(shi)(shi)(shi)(shi)(shi)來考慮,可分(fen)(fen)(fen)為(wei)(wei)中(zhong)心格(ge)(ge)(ge)(ge)(ge)式(shi)(shi)(shi)(shi)(shi)和逆風格(ge)(ge)(ge)(ge)(ge)式(shi)(shi)(shi)(shi)(shi)。考慮時(shi)間(jian)因(yin)子的(de)(de)(de)(de)影響,差(cha)分(fen)(fen)(fen)格(ge)(ge)(ge)(ge)(ge)式(shi)(shi)(shi)(shi)(shi)還可以分(fen)(fen)(fen)為(wei)(wei)顯(xian)格(ge)(ge)(ge)(ge)(ge)式(shi)(shi)(shi)(shi)(shi)、隱格(ge)(ge)(ge)(ge)(ge)式(shi)(shi)(shi)(shi)(shi)、顯(xian)隱交替格(ge)(ge)(ge)(ge)(ge)式(shi)(shi)(shi)(shi)(shi)等。
以隱式有(you)限差(cha)分為例(li),對通式(2-152)進行數(shu)(shu)值離散(san),二階(jie)導數(shu)(shu)采用二階(jie)中心差(cha)商形式,經整理得:

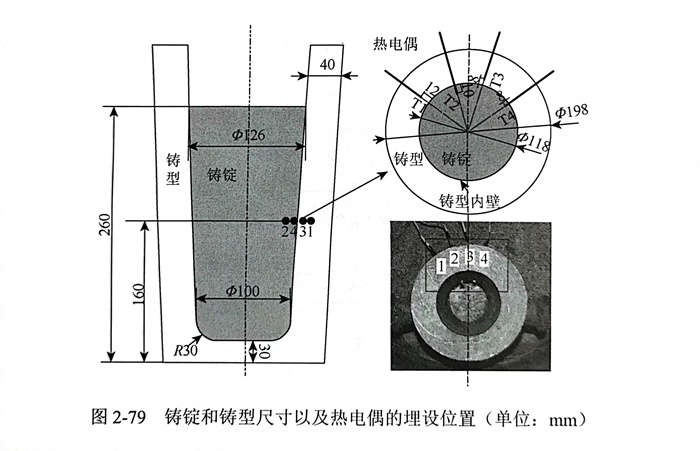
為(wei)了更好地說(shuo)明壓力對(dui)界(jie)面換熱(re)系數的影(ying)響(xiang),以高(gao)氮(dan)鋼P2000加壓凝(ning)固(gu)過(guo)(guo)(guo)程的傳(chuan)熱(re)現(xian)象為(wei)例,采用4根雙鉑銠(B型)熱(re)電(dian)(dian)偶,通過(guo)(guo)(guo)埋設(she)熱(re)電(dian)(dian)偶測(ce)(ce)溫實驗測(ce)(ce)量凝(ning)固(gu)過(guo)(guo)(guo)程鑄(zhu)錠(ding)和鑄(zhu)型溫度變(bian)化曲線,采用兩個位移傳(chuan)感器測(ce)(ce)量凝(ning)固(gu)過(guo)(guo)(guo)程中鑄(zhu)型和鑄(zhu)錠(ding)的位移變(bian)化情(qing)況,獲得凝(ning)固(gu)過(guo)(guo)(guo)程中鑄(zhu)錠(ding)和鑄(zhu)型界(jie)面氣隙演變(bian)規律,測(ce)(ce)量裝置示意圖(tu)(tu)和實物圖(tu)(tu)如圖(tu)(tu)2-79所示。
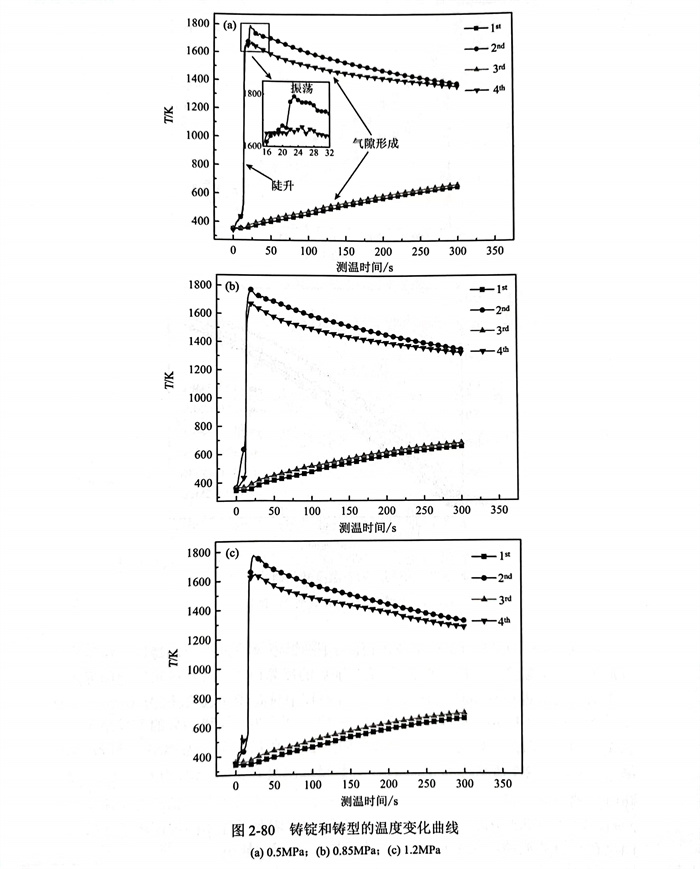
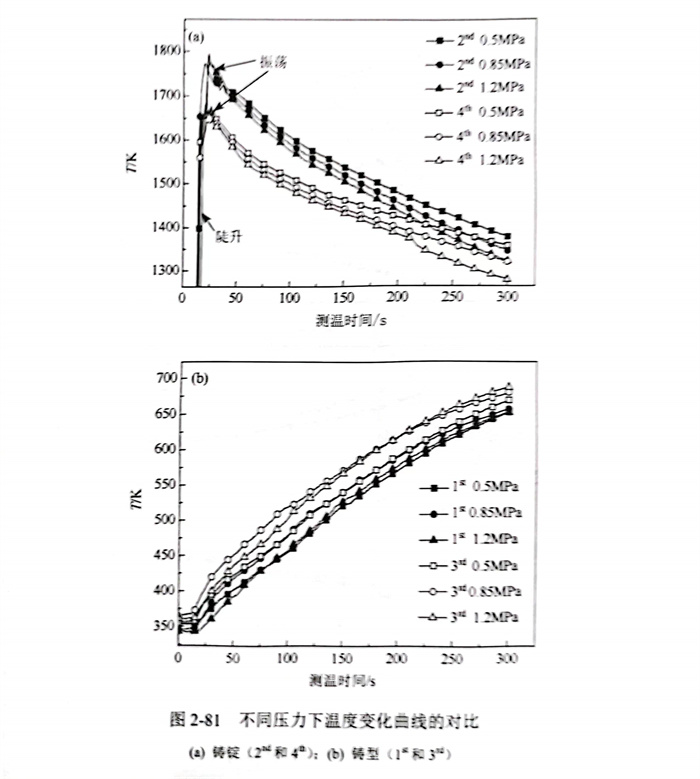
澆注(zhu)(zhu)結(jie)束后,在(zai)0.5MPa、0.85MPa和(he)(he)1.2MPa下(xia)(xia)的(de)鋼(gang)(gang)液凝固過(guo)程中(zhong),鑄(zhu)錠(ding)和(he)(he)鑄(zhu)型(xing)溫(wen)度(du)(du)變(bian)(bian)化(hua)曲線(xian)(xian)(xian)的(de)測量結(jie)果如(ru)圖2-80所(suo)(suo)示,溫(wen)度(du)(du)變(bian)(bian)化(hua)曲線(xian)(xian)(xian)測量的(de)時(shi)間(jian)區間(jian)為(wei)澆注(zhu)(zhu)結(jie)束后的(de)300s以(yi)內,且鑄(zhu)錠(ding)和(he)(he)鑄(zhu)型(xing)在(zai)不同壓力(li)下(xia)(xia)的(de)溫(wen)度(du)(du)變(bian)(bian)化(hua)趨勢基本(ben)一致(zhi)。以(yi)0.5MPa下(xia)(xia)的(de)溫(wen)度(du)(du)變(bian)(bian)化(hua)曲線(xian)(xian)(xian)為(wei)例,如(ru)圖2-80(a)所(suo)(suo)示,在(zai)初始階(jie)段(duan),2nd和(he)(he)4h曲線(xian)(xian)(xian)上溫(wen)度(du)(du)均(jun)存在(zai)陡升和(he)(he)振蕩階(jie)段(duan),這(zhe)(zhe)主要是在(zai)測溫(wen)初期,熱電偶(ou)與鋼(gang)(gang)液接觸(chu)后的(de)自身(shen)預熱,以(yi)及澆注(zhu)(zhu)引起鋼(gang)(gang)液的(de)湍流所(suo)(suo)致(zhi)[104];隨著鋼(gang)(gang)液凝固的(de)進(jin)行,由于鑄(zhu)錠(ding)不斷向(xiang)鑄(zhu)型(xing)傳熱,致(zhi)使(shi)鑄(zhu)錠(ding)的(de)溫(wen)度(du)(du)(2nd和(he)(he)4h)逐漸減小,而鑄(zhu)型(xing)的(de)溫(wen)度(du)(du)(1st和(he)(he)3rd)隨之增加。此(ci)外,測溫(wen)位置相近的(de)3rd和(he)(he)4th曲線(xian)(xian)(xian)之間(jian)存在(zai)較大(da)的(de)溫(wen)差(cha),這(zhe)(zhe)主要是由于鑄(zhu)錠(ding)和(he)(he)鑄(zhu)型(xing)間(jian)氣隙形成后產(chan)生(sheng)的(de)巨(ju)大(da)熱阻Rair-cap(=1/hi),其(qi)中(zhong)h為(wei)鑄(zhu)錠(ding)和(he)(he)鑄(zhu)型(xing)間(jian)的(de)換熱系數。
不(bu)同(tong)壓(ya)力下鑄(zhu)(zhu)(zhu)型(xing)溫度的(de)(de)增(zeng)長(chang)速率(lv)(15t和(he)(he)3rd)和(he)(he)鑄(zhu)(zhu)(zhu)錠的(de)(de)冷(leng)卻速率(lv)(2d和(he)(he)4h)如圖2-81所示,當壓(ya)力從0.5MPa增(zeng)加至(zhi)1.2MPa時,鑄(zhu)(zhu)(zhu)錠內2md和(he)(he)4h熱(re)(re)(re)(re)電偶測(ce)溫點冷(leng)卻速率(lv)的(de)(de)增(zeng)量(liang)(liang)分別(bie)為(wei)0.335K/s和(he)(he)0.605K/s.與此(ci)同(tong)時,在(zai)澆(jiao)注結束后300s時,鑄(zhu)(zhu)(zhu)錠內2d和(he)(he)4h測(ce)溫位置之間的(de)(de)平(ping)均溫度梯度從4.0K/mm增(zeng)加到(dao)了8.6K/mm.由導熱(re)(re)(re)(re)的(de)(de)傅里(li)葉定律(Qingor=αGr,α為(wei)19Cr14Mn0.9N鑄(zhu)(zhu)(zhu)錠的(de)(de)導熱(re)(re)(re)(re)系數,Qingot為(wei)熱(re)(re)(re)(re)通(tong)(tong)量(liang)(liang))可(ke)知,隨(sui)著壓(ya)力的(de)(de)增(zeng)加,鑄(zhu)(zhu)(zhu)錠內沿度梯度方向(xiang)上的(de)(de)熱(re)(re)(re)(re)通(tong)(tong)量(liang)(liang)增(zeng)大。此(ci)外,根據能(neng)量(liang)(liang)守恒(heng)定律(即Q=Qingot,Q為(wei)鑄(zhu)(zhu)(zhu)錠和(he)(he)鑄(zhu)(zhu)(zhu)型(xing)間的(de)(de)熱(re)(re)(re)(re)通(tong)(tong)量(liang)(liang)),鑄(zhu)(zhu)(zhu)錠和(he)(he)鑄(zhu)(zhu)(zhu)型(xing)間的(de)(de)熱(re)(re)(re)(re)通(tong)(tong)量(liang)(liang)也隨(sui)之增(zeng)加。因此(ci),增(zeng)加壓(ya)力能(neng)夠顯著加快鑄(zhu)(zhu)(zhu)錠的(de)(de)冷(leng)卻以及強化鑄(zhu)(zhu)(zhu)錠和(he)(he)鑄(zhu)(zhu)(zhu)型(xing)間的(de)(de)換熱(re)(re)(re)(re)。
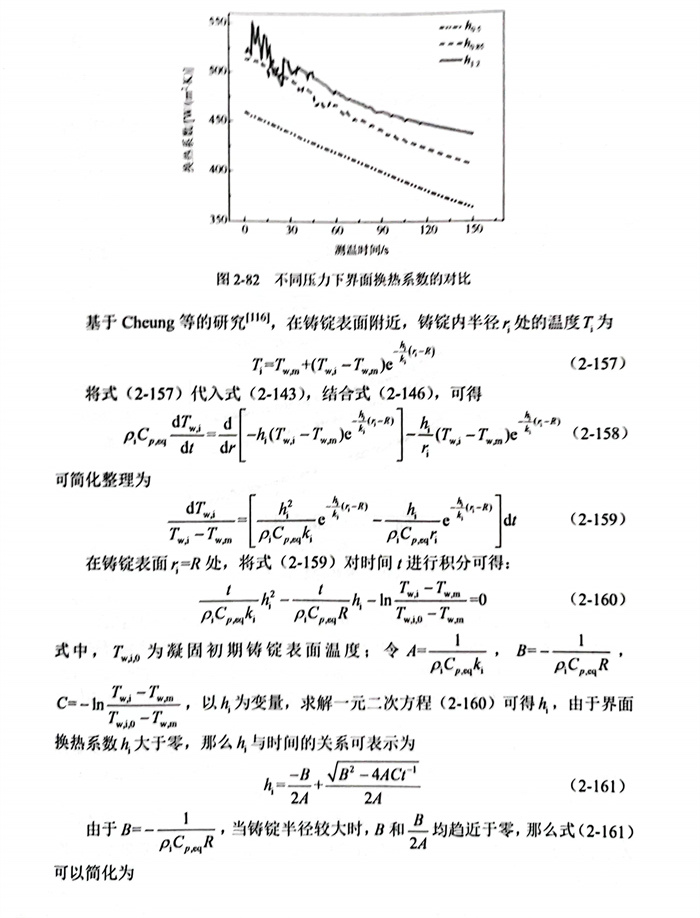
在(zai)0.5MPa、0.85MPa和(he)1.2MPa壓力(li)下的(de)(de)(de)鋼液凝固(gu)過程中(zhong),鑄(zhu)錠(ding)和(he)鑄(zhu)型的(de)(de)(de)溫度測量值作(zuo)為輸入(ru)值(圖2-80),運用驗證后的(de)(de)(de)反(fan)算(suan)(suan)模型,對鑄(zhu)錠(ding)和(he)鑄(zhu)型間(jian)(jian)(jian)(jian)界(jie)面換熱(re)系(xi)數(shu)(shu)隨(sui)時(shi)(shi)間(jian)(jian)(jian)(jian)的(de)(de)(de)變(bian)化規律進行反(fan)算(suan)(suan),反(fan)算(suan)(suan)過程中(zhong)時(shi)(shi)間(jian)(jian)(jian)(jian)步長(chang)(chang)Δt取值為0.75s,空間(jian)(jian)(jian)(jian)步長(chang)(chang)Δr取值為1mm,常數(shu)(shu)β和(he)8分(fen)(fen)別為10-10和(he)200.換熱(re)系(xi)數(shu)(shu)的(de)(de)(de)反(fan)算(suan)(suan)結果分(fen)(fen)別為hos、ho85和(he)h2,隨(sui)時(shi)(shi)間(jian)(jian)(jian)(jian)的(de)(de)(de)變(bian)化規律如(ru)圖2-82所示,由于Δt和(he)8乘積為150s,結合Beck非線性估算(suan)(suan)法(fa)本身(shen)(shen)的(de)(de)(de)特點,只能反(fan)算(suan)(suan)出凝固(gu)前期(qi)150s內hos、ho.85和(he)h2隨(sui)時(shi)(shi)間(jian)(jian)(jian)(jian)的(de)(de)(de)變(bian)化規律。此外,因熱(re)電偶(ou)本身(shen)(shen)的(de)(de)(de)預熱(re)以及澆注引起鋼液的(de)(de)(de)湍流,導致2nd和(he)4th熱(re)電偶(ou)的(de)(de)(de)在(zai)前30s內存(cun)在(zai)較(jiao)大的(de)(de)(de)波(bo)動,因此反(fan)算(suan)(suan)出的(de)(de)(de)界(jie)面換熱(re)系(xi)數(shu)(shu)在(zai)前期(qi)存(cun)在(zai)一定的(de)(de)(de)波(bo)動,其(qi)(qi)中(zhong)h2最(zui)大,其(qi)(qi)次(ci)是(shi)ho.85,ho5最(zui)小(xiao)。
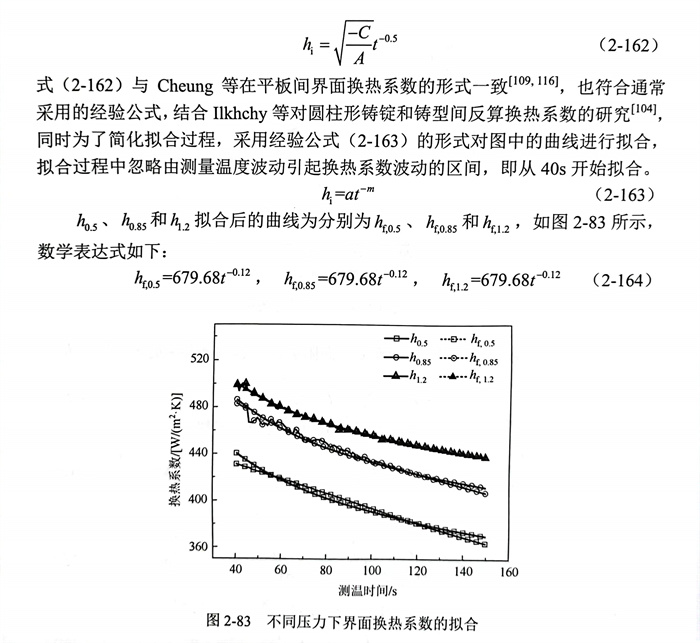
擬(ni)合后的(de)參數Adj.R-Square分(fen)別為0.9558、0.9716和0.9692,說明(ming)擬(ni)合度高,反算結果和經驗公式相符。通過(guo)對(dui)比不同壓力(li)下(xia)反算出的(de)界(jie)面(mian)換(huan)熱系數可知,隨著壓力(li)的(de)增加,界(jie)面(mian)換(huan)熱系數增大,鑄錠和鑄型間界(jie)面(mian)換(huan)熱條件得到明(ming)顯改(gai)善,充分(fen)說明(ming)壓力(li)在19Cr14Mn0.9N含氮鋼的(de)凝(ning)固過(guo)程中(zhong),起到了(le)十(shi)分(fen)顯著的(de)強(qiang)化(hua)冷卻作(zuo)用。
眾所(suo)周知,在(zai)某一時刻下,界面(mian)換(huan)(huan)熱(re)系(xi)數與(yu)壓力呈現多項式(shi)關(guan)系(xi)。為了(le)獲得19Cr14Mn0.9N 含氮鋼界面(mian)換(huan)(huan)熱(re)系(xi)數與(yu)壓力之間的關(guan)系(xi),可采用多項式(shi)擬(ni)合的方式(shi)對(dui)界面(mian)換(huan)(huan)熱(re)系(xi)數與(yu)壓力關(guan)系(xi)進行擬(ni)合,擬(ni)合關(guan)系(xi)式(shi)為



