奧氏體不銹鋼應(ying)力腐蝕開裂過程可分為兩個階段,是金屬表面鈍(dun)化(hua)腺破壞引發點蝕;二是點蝕坑發展為裂紋。源于點蝕(shi)的應力腐蝕破壞鏈可以分為五個基本過程,如圖1-1所示。

點蝕(shi)與應(ying)力腐蝕(shi)緊密相關(guan),作為應(ying)力腐蝕(shi)裂(lie)紋的重要起源,90多(duo)年來,人(ren)們(men)對點蝕(shi)的研究(jiu)一直沒(mei)(mei)有中斷,然而,至今為止點蝕(shi)機(ji)理及(ji)預防(fang)并(bing)沒(mei)(mei)有完全(quan)弄清(qing)楚。
1. 機理
對于點蝕形核機理,學者們已做了大量研究。1998年,Frankel 從熱力學和動力學兩方面對點蝕的機理做了大量的闡述,并分析了合金成分和微觀結構、腐蝕介質的組成及溫度等對點蝕的影響。文獻從亞穩態點蝕的形核機理、生長、向穩態點蝕轉化等幾個方面,總結了近年來的研究成果。2015年,Soltis 從點蝕特征、鈍化膜(mo)破裂機理、點蝕生長、點蝕坑的演化及點蝕形貌等方面,全面綜述了人們對點蝕90多年的研究成果。奧氏體不銹鋼點蝕的形成是由于鈍化膜發生了局部破裂。目前,有關鈍化膜破裂的機理主要有三類:穿透機理、斷裂機理和吸附機理。穿透機理的觀點是:侵蝕性陰離子能夠穿透氧化膜,破壞了氧化膜的完整性,陰離子進入材料基體后引起金屬溶解。與Br-和I-比較,氯離子的直徑較小,更容易穿透氧化膜,因此,對于Fe和Ni合金材料,氯離子是最具侵蝕性的陰離子。斷裂機理認為,當金屬處于含有侵蝕性陰離子的環境時,由界面張力、電致伸縮壓力、靜電壓力等所造成的鈍化膜機械應力破壞先于金屬溶解的發生。吸附機理認為,侵蝕性陰離子吸附在氧化膜表面,促進了氧化膜中的金屬離子向電解液轉移,使鈍化膜表面引起局部表面減薄,并最終導致局部溶解。
每種膜破裂機理都有一定的理論依據,但也有被質疑的一面。因此,有學者提出了一些其他的點蝕形核理論,例如局部酸化理論、金屬-氧化物邊界空洞理論、電擊穿理論等。點蝕的產生既受材料影響又受環境影響,因此,鈍化膜的破壞可能受多種機制的共同控制。以上機理的提出都是基于純金屬體系。然而,任何一種材料的表面都不是光滑完整的,對于不銹鋼而言,表面存在夾雜物、沉淀等活性點,這些活性點是誘導點蝕萌生的關鍵因素。研究人員普遍認為,不銹鋼金屬的點蝕優先從硫化物夾雜部位萌生,并通過不同的實驗方法來解釋這一現象。2007年,Oltra等采用微型電化學探測技術和有限元模擬方法,從應力的角度解釋了點蝕萌生于MnS夾雜處的原因,他認為由于MnS夾雜物彈性模量和基體材料彈性模量相差很大,在夾雜物周圍產生一定的應力梯度,進而促進了金屬的溶解。Zheng等采用透射電鏡觀察,發現不(bu)銹鋼夾雜物MnS中含有MnCr2O4納米顆粒,這類顆粒的結構為八面體;同時,研究發現,MnS與MnCr2O4顆粒的界面優先溶解,最終引起MnS溶解,這一發現解釋了為什么MnS處常常為點蝕位置。而Chiba等通過原位觀察則認為點蝕都是起源于MnS夾雜與基體材料的接觸部位,這是因為氯離子環境中MnS的溶解導致了S元素在夾雜物周圍沉積,S元素和Cl-的協同作用使夾雜物周圍的基體材料溶解。
2. 影(ying)響因素
影響(xiang)(xiang)不銹(xiu)鋼點蝕(shi)(shi)形(xing)(xing)核的(de)(de)因(yin)素很多,除了材料(liao)(liao)表(biao)面夾雜,還(huan)有材料(liao)(liao)化(hua)學(xue)(xue)成分和微觀結構,腐(fu)蝕(shi)(shi)介質的(de)(de)組成、溫度和流動狀態,以(yi)及設備的(de)(de)幾何(he)結構等(deng)(deng)因(yin)素。另外(wai),受(shou)力(li)狀態對(dui)點蝕(shi)(shi)的(de)(de)形(xing)(xing)成也有一定影響(xiang)(xiang)。在(zai)存(cun)在(zai)應(ying)力(li)的(de)(de)情況下,林(lin)昌健等(deng)(deng)對(dui)奧氏體不銹(xiu)鋼腐(fu)蝕(shi)(shi)電化(hua)學(xue)(xue)行為進(jin)行了研究(jiu),結果發(fa)(fa)現(xian)力(li)學(xue)(xue)因(yin)素可(ke)使表(biao)面腐(fu)蝕(shi)(shi)電化(hua)學(xue)(xue)活性(xing)增加(jia),點蝕(shi)(shi)可(ke)優先(xian)發(fa)(fa)生(sheng)(sheng)在(zai)應(ying)力(li)集中位置。對(dui)于(yu)均勻(yun)材料(liao)(liao),Martin等(deng)(deng)發(fa)(fa)現(xian)79%的(de)(de)點蝕(shi)(shi)起源于(yu)機械拋光引起的(de)(de)應(ying)變硬化(hua)區域(yu)。Yuan等(deng)(deng)也發(fa)(fa)現(xian),較大的(de)(de)外(wai)加(jia)拉應(ying)力(li)對(dui)點蝕(shi)(shi)的(de)(de)發(fa)(fa)生(sheng)(sheng)有促進(jin)作用。Shimahashi等(deng)(deng)通過微型電化(hua)學(xue)(xue)測量研究(jiu)了外(wai)應(ying)力(li)對(dui)點蝕(shi)(shi)萌生(sheng)(sheng)的(de)(de)影響(xiang)(xiang),結果表(biao)明外(wai)加(jia)拉應(ying)力(li)促進(jin)了MnS溶解,導致(zhi)點蝕(shi)(shi)形(xing)(xing)成,甚至是裂紋的(de)(de)產生(sheng)(sheng)。
3. 隨機特性
隨著對點蝕的深入研究,人們逐漸認識到點蝕的萌生和生長具有很大隨機性。20世紀70年代末是點蝕隨機性研究集中期,有相當多的學者對于點蝕的隨機性問題進行了深入研究。1977年,Shibata等利用304不銹(xiu)鋼在氯化鈉溶液中的電化學實驗數據,采用隨機理論分析了點蝕電位和點蝕誘導時間的統計特性。研究表明:點蝕電位服從正態分布,通過分析不同時間內的點蝕數量,提出了點蝕生滅的隨機過程。Shibata等總共提出了6種不同的點蝕生滅過程,并在后來的工作中基于鈍化膜的點缺陷模型,進一步研究了點蝕生滅的隨機過程。1994年,文獻的作者提出了點蝕的分布函數理論,這些模型有助于解釋實驗結果。Williams 等把點蝕過程作為隨機事件,并考慮點蝕的生滅過程,建立了點蝕萌生的隨機模型,他認為穩態點蝕的生成概率可以表示為:
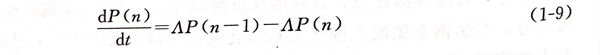
式中,A為(wei)穩態(tai)點(dian)蝕的萌(meng)生率。
Laycock等對 Williams的(de)(de)(de)(de)模型(xing)進行了(le)(le)修正,他(ta)認為在實(shi)際情況中,研究(jiu)最(zui)大點(dian)(dian)(dian)(dian)蝕(shi)(shi)(shi)尺寸(cun)是很重要的(de)(de)(de)(de),他(ta)們的(de)(de)(de)(de)研究(jiu)結果表明(ming)點(dian)(dian)(dian)(dian)蝕(shi)(shi)(shi)坑深(shen)度(du)(du)隨(sui)時(shi)間呈(cheng)指數(shu)關系增長,并(bing)采用4參數(shu)的(de)(de)(de)(de)廣義極(ji)值分(fen)(fen)布預(yu)測了(le)(le)最(zui)大點(dian)(dian)(dian)(dian)蝕(shi)(shi)(shi)深(shen)度(du)(du)的(de)(de)(de)(de)發展規律(lv)。1988年,Baroux 認為點(dian)(dian)(dian)(dian)蝕(shi)(shi)(shi)萌生(sheng)(sheng)(sheng)率是氯離子濃(nong)度(du)(du)、溫度(du)(du)以及(ji)不(bu)銹鋼類型(xing)的(de)(de)(de)(de)函數(shu),在不(bu)考(kao)慮(lv)實(shi)際鈍化膜(mo)破裂(lie)機(ji)理的(de)(de)(de)(de)前提下,建(jian)立(li)了(le)(le)有關點(dian)(dian)(dian)(dian)蝕(shi)(shi)(shi)萌生(sheng)(sheng)(sheng)的(de)(de)(de)(de)動力學(xue)隨(sui)機(ji)模型(xing)。1997年,Wu等考(kao)慮(lv)了(le)(le)亞(ya)穩(wen)態(tai)點(dian)(dian)(dian)(dian)蝕(shi)(shi)(shi)和(he)穩(wen)態(tai)點(dian)(dian)(dian)(dian)蝕(shi)(shi)(shi)之(zhi)間的(de)(de)(de)(de)相(xiang)(xiang)互(hu)(hu)作用,建(jian)立(li)了(le)(le)點(dian)(dian)(dian)(dian)蝕(shi)(shi)(shi)產生(sheng)(sheng)(sheng)的(de)(de)(de)(de)隨(sui)機(ji)模型(xing),認為每(mei)個亞(ya)穩(wen)態(tai)的(de)(de)(de)(de)點(dian)(dian)(dian)(dian)蝕(shi)(shi)(shi)時(shi)間會影響隨(sui)后的(de)(de)(de)(de)事(shi)件,并(bing)且這種影響隨(sui)時(shi)間而衰減(jian)。點(dian)(dian)(dian)(dian)蝕(shi)(shi)(shi)的(de)(de)(de)(de)產生(sheng)(sheng)(sheng)不(bu)是孤立(li)的(de)(de)(de)(de),相(xiang)(xiang)鄰點(dian)(dian)(dian)(dian)蝕(shi)(shi)(shi)之(zhi)間的(de)(de)(de)(de)相(xiang)(xiang)互(hu)(hu)作用會導致穩(wen)態(tai)點(dian)(dian)(dian)(dian)蝕(shi)(shi)(shi)的(de)(de)(de)(de)突(tu)然發生(sheng)(sheng)(sheng)。Harlow通過材料表面離子團尺寸(cun)、分(fen)(fen)布、化學(xue)成分(fen)(fen)的(de)(de)(de)(de)隨(sui)機(ji)性,研究(jiu)了(le)(le)點(dian)(dian)(dian)(dian)蝕(shi)(shi)(shi)萌生(sheng)(sheng)(sheng)以及(ji)生(sheng)(sheng)(sheng)長的(de)(de)(de)(de)隨(sui)機(ji)過程。
1989年,Provan等(deng)在(zai)(zai)不考慮點(dian)蝕(shi)(shi)產(chan)生(sheng)過(guo)(guo)程(cheng)的(de)(de)情況下(xia),首先提出(chu)了(le)點(dian)蝕(shi)(shi)深度(du)(du)增長(chang)的(de)(de)非齊次馬(ma)(ma)爾(er)科(ke)夫過(guo)(guo)程(cheng)模(mo)(mo)(mo)型。1999年,Hong將表示點(dian)蝕(shi)(shi)產(chan)生(sheng)過(guo)(guo)程(cheng)的(de)(de)泊松模(mo)(mo)(mo)型與(yu)(yu)表示點(dian)蝕(shi)(shi)增長(chang)的(de)(de)馬(ma)(ma)爾(er)科(ke)夫過(guo)(guo)程(cheng)模(mo)(mo)(mo)型相互(hu)結合形成(cheng)組合模(mo)(mo)(mo)型,這是第一(yi)次將點(dian)蝕(shi)(shi)的(de)(de)萌發過(guo)(guo)程(cheng)與(yu)(yu)生(sheng)長(chang)過(guo)(guo)程(cheng)結合在(zai)(zai)一(yi)起進(jin)行研(yan)究(jiu)(jiu)。2007年,Valor等(deng)在(zai)(zai)文(wen)獻的(de)(de)研(yan)究(jiu)(jiu)基礎上,改(gai)進(jin)了(le)馬(ma)(ma)爾(er)科(ke)夫模(mo)(mo)(mo)型,通過(guo)(guo)Gumbel極值分(fen)(fen)布把眾多點(dian)蝕(shi)(shi)坑的(de)(de)產(chan)生(sheng)與(yu)(yu)擴展聯合在(zai)(zai)一(yi)起研(yan)究(jiu)(jiu)。2013年,Valor等(deng)分(fen)(fen)別使用兩個(ge)不同的(de)(de)馬(ma)(ma)爾(er)科(ke)夫鏈模(mo)(mo)(mo)擬了(le)地下(xia)管道(dao)的(de)(de)外部點(dian)蝕(shi)(shi)過(guo)(guo)程(cheng)和點(dian)蝕(shi)(shi)試驗中最大(da)點(dian)蝕(shi)(shi)深度(du)(du)。
Turnbull等(deng)根據實驗(yan)結果(guo)(guo),對(dui)點(dian)蝕(shi)(shi)(shi)的(de)(de)(de)發(fa)展(zhan)規律進行了(le)統計(ji)學分(fen)析,對(dui)于點(dian)蝕(shi)(shi)(shi)坑(keng)深(shen)(shen)度(du)(du)的(de)(de)(de)變(bian)(bian)化,建立了(le)一(yi)方(fang)程(cheng)(cheng),并(bing)(bing)給出了(le)點(dian)蝕(shi)(shi)(shi)深(shen)(shen)度(du)(du)隨(sui)時(shi)間(jian)呈指數(shu)(shu)變(bian)(bian)化的(de)(de)(de)關(guan)系式,該模(mo)(mo)型屬于典型的(de)(de)(de)隨(sui)機(ji)變(bian)(bian)量模(mo)(mo)型,未涉及點(dian)蝕(shi)(shi)(shi)坑(keng)萌(meng)(meng)生(sheng)數(shu)(shu)量。Caleyo等(deng)研究(jiu)了(le)地下(xia)管道(dao)點(dian)蝕(shi)(shi)(shi)坑(keng)深(shen)(shen)度(du)(du)和(he)(he)生(sheng)長(chang)速率(lv)(lv)(lv)的(de)(de)(de)概(gai)率(lv)(lv)(lv)分(fen)布,結果(guo)(guo)發(fa)現,在相對(dui)較(jiao)短的(de)(de)(de)暴(bao)露時(shi)間(jian)內,Weibull和(he)(he)Gumbel分(fen)布適合描述點(dian)蝕(shi)(shi)(shi)深(shen)(shen)度(du)(du)和(he)(he)生(sheng)長(chang)速率(lv)(lv)(lv)的(de)(de)(de)分(fen)布;而(er)在較(jiao)長(chang)的(de)(de)(de)時(shi)間(jian)內,Fréchet分(fen)布最適合。Datla等(deng)把點(dian)蝕(shi)(shi)(shi)的(de)(de)(de)萌(meng)(meng)生(sheng)過(guo)程(cheng)(cheng)看作泊(bo)松過(guo)程(cheng)(cheng),點(dian)蝕(shi)(shi)(shi)坑(keng)的(de)(de)(de)尺寸看成滿足(zu)廣(guang)義帕雷托分(fen)布的(de)(de)(de)隨(sui)機(ji)變(bian)(bian)量,并(bing)(bing)用(yong)來估算蒸汽發(fa)生(sheng)管泄漏(lou)的(de)(de)(de)概(gai)率(lv)(lv)(lv)。Zhou等(deng)基于隨(sui)機(ji)過(guo)程(cheng)(cheng)理論,運用(yong)非(fei)齊次泊(bo)松過(guo)程(cheng)(cheng)和(he)(he)非(fei)定態伽馬過(guo)程(cheng)(cheng)模(mo)(mo)擬(ni)了(le)點(dian)蝕(shi)(shi)(shi)產生(sheng)和(he)(he)擴(kuo)展(zhan)兩(liang)個過(guo)程(cheng)(cheng)。在Shekari等(deng)提出的(de)(de)(de)“合于使用(yong)評價(jia)”方(fang)法中,把點(dian)蝕(shi)(shi)(shi)密度(du)(du)作為非(fei)齊次泊(bo)松過(guo)程(cheng)(cheng),最大點(dian)蝕(shi)(shi)(shi)深(shen)(shen)度(du)(du)作為非(fei)齊次馬爾科夫過(guo)程(cheng)(cheng),采(cai)用(yong)蒙特(te)卡羅(luo)法和(he)(he)一(yi)次二階矩法模(mo)(mo)擬(ni)了(le)可靠性指數(shu)(shu)和(he)(he)點(dian)蝕(shi)(shi)(shi)失效概(gai)率(lv)(lv)(lv)。
點(dian)蝕隨(sui)機(ji)性(xing)的(de)研究(jiu)主要集中(zhong)在點(dian)蝕萌生和生長兩方面,隨(sui)機(ji)變(bian)量(liang)模型(xing)的(de)優點(dian)在于能夠結合機(ji)理(li),然(ran)而一旦(dan)機(ji)理(li)不清,隨(sui)機(ji)性(xing)分析將很難進行;隨(sui)機(ji)過(guo)程模型(xing)是把系(xi)統退(tui)化(hua)看(kan)作(zuo)完(wan)全隨(sui)機(ji)的(de)過(guo)程,系(xi)統退(tui)化(hua)特征值隨(sui)時(shi)間的(de)變(bian)化(hua)情(qing)況可以通(tong)過(guo)模擬(ni)直接(jie)獲得,但(dan)受(shou)觀測手段的(de)限(xian)制,試(shi)驗周期長,操作(zuo)難度大。



